[BDA 데이터 분석 모델링반 (ML 1) 5회차] KNN 알고리즘
KNN 알고리즘에 대해 알아보고, 실습을 통해 KNN 알고리즘의 파라미터, 최적의 k를 찾아본다.
KNN(K-Nearest Neighbors)
KNN은 데이터로부터 가까운 거리에 있는 k개의 다른 데이터에 의한 결과로 예측하는 알고리즘을 말한다.
회귀 문제와 분류 문제 모두 해결 가능한 Memory-based learning이다.
k 결정 과정
너무 큰 k를 선택하면, 미세한 경계부분의 분류 정확도가 떨어지게 되며,
너무 작은 k를 선택하면, 과적합이 될 가능성이 생기며, 이상치의 영향을 크게 받고, 패턴이 직관적이지 못한다.
Majority voting
데이터의 갯수가 균일하지 않다면, 거리에 반비례하는 Weight를 주어 편향성의 영향을 줄일 수 있다.
종속변수
범주형 변수
KNN 중 가장 많이 나타나는 범주로 y를 추정하며, Tie 문제를 막기 위해 k는 홀수로 정하는 것이 좋다.
$$\hat{p}_{m} = \frac{\sum_{i=1}^{k}(Y_{i}=m)}{k}$$
$$\hat{y} = \mathrm{argmax}(\hat{p}_{m})$$
$$m = 1,\cdots , M$$
연속형 변수
KNN의 대푯값(평균)으로 y를 추정(근처 k개의 평균을 선택)한다.
$$\hat{y} = \frac{\sum_{i=1}^{k}Y_{(i)}}{k}$$
Inverse distance weighted average 고려 가능하다.
$$\hat{y} = \frac{\sum_{i=1}^{k}\frac{1}{d(X_{(i)}, x)}\cdot Y_{(i)}}{k}$$
설명 변수
범주형 변수
Hamming distance
$D_{H} = \sum_{j=1}^{J}I (x_{j}\neq y_{j})$
J개의 연속형 변수
Euclidian distance
$D_{E} = \sqrt{\sum_{j=1}^{J}(x_j-y_j)^{2}}$
Manhattan distance
$D_{M} = \sum_{j=1}^{J}|x_j-y_j|^{2}$
KNN 알고리즘 실습
파라미터 종류
n_neighbors : 판단에 사용할 이웃한 값의 갯수(k값)
weights : 이웃 값들의 가중치 결정방법, 기본값은 uniform(동일한 가중치), distance(거리에 반비례하는 가중치)
metric : 거리 측정 방식 (ex. euclidean, manhanttan)
algorithm : 거리 기반으로 어떻게 탐색할 것인가?
auto) 가장 적정한 것을 골라 데이터 차원, 패턴에 따라서 자동으로 탐색하는 것
ball_tree) 필요한 부분을 빠르게 탐색하기 위한 방법
kd_tree) 데이터 구조, 분할방식으로 차원을 축소하면서 진행하는 방법
brute) 완전탐색방식으로 가장 직관적인 방법, 데이터가 크면 계산량이 증가한다.
가중치에 따라 학습 결과가 어떻게 변화하는지 확인해본다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import neighbors
np.random.seed(0)
X = np.sort(5 * np.random.rand(40, 1), axis=0)
T = np.linspace(0, 5, 500)[:, np.newaxis]
y = np.sin(X).ravel()
# Add noise to targets
y[::5] += 1 * (0.5 - np.random.rand(8))n_neighbors = 5
for i, weights in enumerate(["uniform", "distance"]):
knn = neighbors.KNeighborsRegressor(n_neighbors, weights=weights)
y_ = knn.fit(X, y).predict(T)
plt.subplot(2, 1, i + 1)
plt.scatter(X, y, color="darkorange", label="data")
plt.plot(T, y_, color="navy", label="prediction")
plt.axis("tight")
plt.legend()
plt.title("KNeighborsRegressor (k = %i, weights = '%s')" % (n_neighbors, weights))
plt.tight_layout()
plt.show()
캘리포니아 데이터를 활용하여 KNN 알고리즘의 회귀, 분류, 이상치 탐지 등을 확인해본다.
from sklearn.neighbors import KNeighborsRegressor
X,y = fetch_california_housing(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.3, random_state=111)
적당한(MSE 값이 가장 낮은) k의 값을 찾는다.
k_values = range(1,20)
mse_scores = []
for k in k_values:
knn = KNeighborsRegressor(n_neighbors=k)
scores = cross_val_score(knn, X_train, y_train, cv=3, scoring='neg_mean_squared_error')
mse_scores.append(-scores.mean())
optimal_k = k_values[mse_scores.index(min(mse_scores))]
print(f'Optimal K: {optimal_k}')
#Optimal K: 9
# MSE 간단한 시각화를 통해 살펴보자!
plt.figure(figsize=(15,8))
plt.plot(k_values, mse_scores, marker='o')
특정 k 값이 도달한 이후에 MSE는 점점 증가한다.
k 값이 증가하면, 모델이 불필요한 패턴까지 학습하고(과적합), 이상치 영향을 더 많이 받게 되어 MSE 값이 올라간다.
Iris 데이터를 KNN을 활용하여 분류해본다.
iris = load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.3, random_state=111)
knn_clf=KNeighborsClassifier(n_neighbors=3)
knn_clf.fit(X_train,y_train)
y_pred = knn_clf.predict(X_test) # 예측값
print('정확도', accuracy_score(y_test, y_pred))
# 정확도 0.9555555555555556
k의 값에 따라 정확도가 어떻게 변하는지 확인해본다.
k_range = range(1,20)
scores = []
for k in k_range:
knn = knn_clf=KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train, y_train)
scores.append(knn.score(X_test, y_test))
plt.figure(figsize=(12,6))
plt.scatter(k_range, scores)
plt.plot(k_range, scores)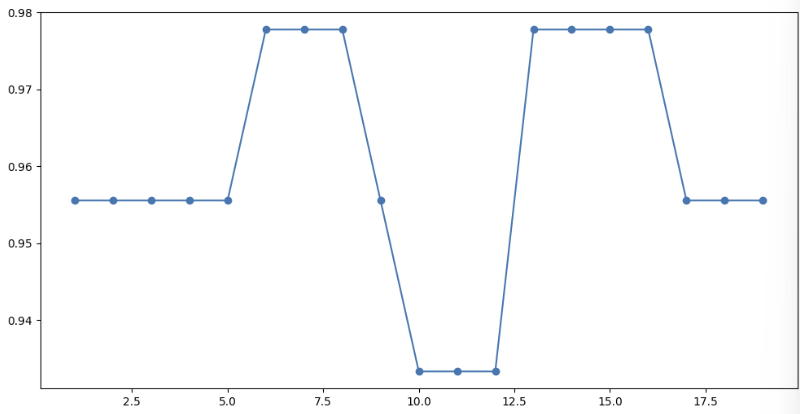
교차검증을 통해 모델을 정교하게 학습해본다.
k_range = range(1,20)
cv_scores = []
for k in k_range:
knn = knn_clf=KNeighborsClassifier(n_neighbors=k)
scores = cross_val_score(knn, X, y, cv=5)
cv_scores.append(scores.mean())
optimal_k = k_range[cv_scores.index(max(cv_scores))]
print(f'Optimal K: {optimal_k}')
# Optimal K: 6
plt.figure(figsize=(12,6))
plt.plot(k_range, cv_scores, marker='o')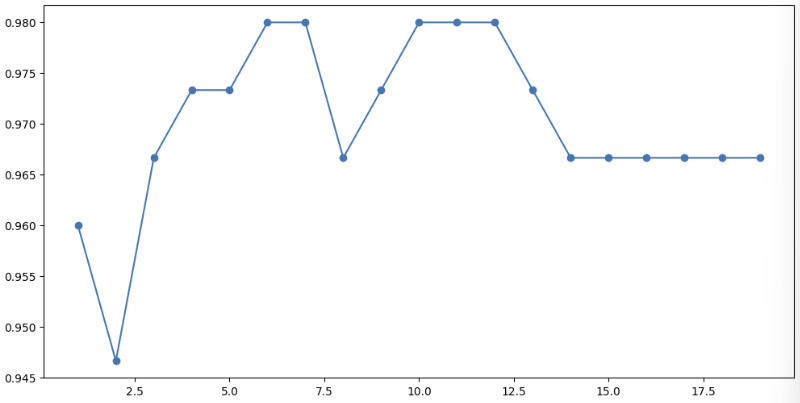
그리드서치로 최적의 k 값을 찾아본다.
from sklearn.model_selection import GridSearchCV
# 하이퍼파라미터
param_grid = {'n_neighbors':range(1,20),'weights':['uniform','distance']}
#grid_search
grid_search = GridSearchCV(KNeighborsClassifier(), param_grid, cv=3, scoring='accuracy')
grid_search.fit(X_train, y_train)
#최적의 하이퍼파라미터
print('최적의 하이퍼 파라미터:', grid_search.best_params_)
print('최적의 스토어:', grid_search.best_score_)
'''
최적의 하이퍼 파라미터: {'n_neighbors': 5, 'weights': 'uniform'}
최적의 스토어: 0.980952380952381
'''
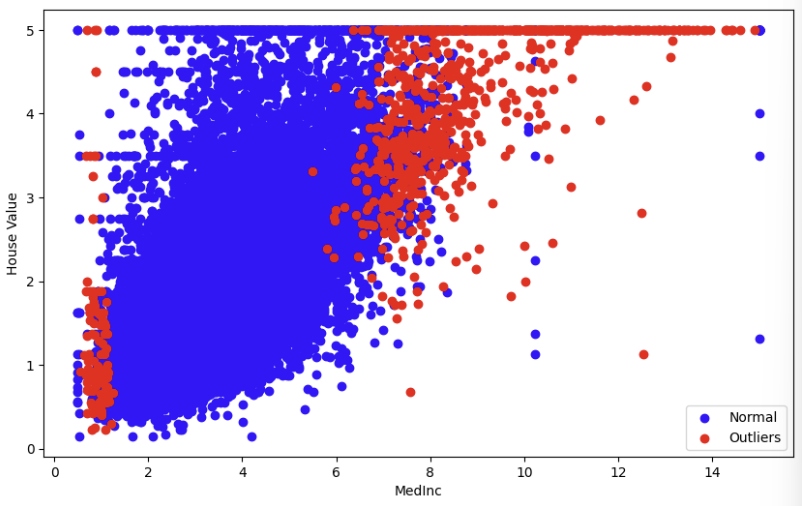
캘리포니아 데이터를 활용하여 이상치를 탐지해본다.
from sklearn.neighbors import NearestNeighbors
cal = fetch_california_housing()
X= cal.data
y= cal.target
## MedInc 집값 컬럼 0번째 컬럼
X_MedInc = X[:,0].reshape(-1,1) # 집값 데이터만 추출
#Knn 모델로 이웃이 5개 거리 계산해서 이상치 탐지해보자
nbrn = NearestNeighbors(n_neighbors = 5, algorithm='ball_tree').fit(X_MedInc)
distance, indices = nbrn.kneighbors(X_MedInc)
# 거리기준으로 이상치 점수 계산해서
outlier_scores = distance[:,-1] # 가장 먼 이웃까지의 거리
# 이상치 점수가 특정 임계값을 넘으면 이상치로 판단
# 상위 5% 이상치 간주하자!
thres = np.percentile(outlier_scores, 95)
is_outlier = outlier_scores > thres
## outlier 시각화 하기
plt.figure(figsize=(10,6))
plt.scatter(X_MedInc[~is_outlier], y[~is_outlier], color='blue', label= 'Normal')
plt.scatter(X_MedInc[is_outlier], y[is_outlier], color='red', label= 'Outliers')
plt.xlabel('MedInc')
plt.ylabel('House Value')
plt.legend()