| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 |
- 로지스틱
- 지니계수
- 규제
- 머신러닝
- 빅데이터분석학회
- Machine Learning
- ML
- OLS
- 한국산업경영시스템학회
- DT
- 가지치기
- AutoML
- 부스팅
- BDA학회
- confusion_matrix
- dl
- 엔트로피
- 논문리뷰
- AAAI
- 에이다부스트
- BDA
- 로짓
- adaboost
- distillm
- 랜덤포레스트
- 데이터사이언스
- skld
- 선형회귀
- 평가지표
- 의사결정트리
- Today
- Total
데이터 사이언스 공부할래
[BDA 데이터 분석 모델링반 (ML 1) 10회차] 다항회귀, 다중회귀 본문
다항/다중회귀에 대해 알아보고, 캘리포니아 주택 데이터를 활용하여 선형/다항/다중회귀에 대한 OLS를 비교해본다.
다항회귀
독립변수의 2차, 3차 방정식과 같은 다항식으로 표현하는 회귀 분석으로, 종속 변수와 독립 변수 간의 비선형 관계를 다항식 형태로 모델링하는 방법이다. 다항회귀는 과적합을 막기 위해 규제가 필요하다. (규제에 관해서는 다음 주차에서 다룬다.)
다항회귀는 비선형회귀가 이닌, 선형회귀이다. 회귀에서 선형과 비선형 회귀를 나누는 기준은 회귀 계수가 선형과 비선형인지에 따라 다른 것이며, 독립변수의 선형과 비선형 여부와는 상관 없다.
다변량 다항 회귀 (Multivariate Polynomial Regression): 여러 개의 독립 변수와 그들의 다항항을 포함하여 종속 변수와의 관계를 모델링하는 방법
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
# 데이터 생성
np.random.seed(0)
x = 2 - 3 * np.random.normal(0, 1, 100)
y = x - 2 * (x ** 2) + np.random.normal(-3, 3, 100)
# 다항 회귀 모델 생성
polynomial_features = PolynomialFeatures(degree=2)
x_poly = polynomial_features.fit_transform(x.reshape(-1, 1))
model = LinearRegression()
model.fit(x_poly, y)
y_poly_pred = model.predict(x_poly)
# 시각화
plt.scatter(x, y, s=10)
plt.plot(np.sort(x), y_poly_pred[np.argsort(x)], color='m')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Polynomial Regression')
plt.show()
다중회귀
하나의 종속 변수와 둘 이상의 독립 변수 간의 관계를 분석하는 회귀 분석이다.
독립 변수들간의 다중공선성이 불안정성을 초래할 수 있어 VIF(Variance Inflation Factor)를 사용하여 진단한다.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 데이터 생성
np.random.seed(0)
x1 = np.random.rand(100)
x2 = np.random.rand(100)
y = 3 + 2 * x1 + 4 * x2 + 1.5 * x1**2 + 0.5 * x2**2 + 2 * x1 * x2 + np.random.normal(0, 0.5, 100)
# 데이터프레임 생성
df = pd.DataFrame({'x1': x1, 'x2': x2, 'y': y})
# 독립 변수와 종속 변수 분리
X = df[['x1', 'x2']]
y = df['y']
# 다항 특성 생성
polynomial_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = polynomial_features.fit_transform(X)
# 다항 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(X_poly, y)
# 회귀 계수 출력
print('Intercept:', model.intercept_)
print('Coefficients:', model.coef_)
# 예측
y_poly_pred = model.predict(X_poly)
# 성능 평가
from sklearn.metrics import mean_squared_error, r2_score
print('Mean Squared Error:', mean_squared_error(y, y_poly_pred))
print('R^2 Score:', r2_score(y, y_poly_pred))
# 시각화 (2차원 공간에서의 예측 시각화)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# 실제 데이터
scat = ax.scatter(df['x1'], df['x2'], df['y'], color='b', label='Actual Data')
# 예측값 시각화
x1_grid, x2_grid = np.meshgrid(np.linspace(0, 1, 100), np.linspace(0, 1, 100))
X_grid_poly = polynomial_features.transform(np.column_stack([x1_grid.ravel(), x2_grid.ravel()]))
y_grid_pred = model.predict(X_grid_poly).reshape(x1_grid.shape)
# 예측 표면
surf = ax.plot_surface(x1_grid, x2_grid, y_grid_pred, color='m', alpha=0.5)
# 축 레이블
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('y')
plt.title('Multivariate Polynomial Regression')
# 범례 추가
actual_proxy = plt.Line2D([0], [0], linestyle="none", marker='o', color='b')
predicted_proxy = plt.Line2D([0], [0], linestyle="none", marker='o', color='m', alpha=0.5)
ax.legend([actual_proxy, predicted_proxy], ['Actual Data', 'Predicted Surface'], numpoints=1)
plt.show()
캘리포니아 주택 가격 데이터를 활용하여 단순 선형회귀와 다항회귀 각각에 대한 MSE, MAE, R2, OLS를 비교해본다.
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error, r2_score
import statsmodels.api as sm
import matplotlib.pyplot as plt
# 캘리포니아 주택 가격 데이터 로드
california = fetch_california_housing()
# 데이터프레임 생성
df = pd.DataFrame(california.data, columns=california.feature_names)
df['MedHouseVal'] = california.target
#MedHouseVal y값
#MedInc 수입의 중앙값
## 단순 선형회귀 분석을 진행
X = df[['MedInc']]
y = df['MedHouseVal']
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.2, random_state=111)## 단순선형회귀
linear_model =LinearRegression()
linear_model.fit(X_train, y_train)
y_pred_linear = linear_model.predict(X_test) #예측값이 출력
## OLS 분석
X_train_ols = sm.add_constant(X_train)
X_test_ols = sm.add_constant(X_test)
ols_model = sm.OLS(y_train,X_train_ols).fit()
y_pred_ols = ols_model.predict(X_test_ols)
##평가지표를 불러오기
mse_linear =mean_squared_error(y_test, y_pred_linear)
r2_linear = r2_score(y_test, y_pred_linear)
mse_ols_linear = mean_squared_error(y_test, y_pred_ols)
r2_ols_linear = r2_score(y_test, y_pred_ols)#ols, sklearn 동일한 값이 출력
print(mse_linear)
print(mse_ols_linear)
print(r2_linear)
print(r2_ols_linear)
'''
0.7282634839897112
0.7282634839897112
0.45589490363155005
0.45589490363155005
'''#다항회귀 추가
poly_features =PolynomialFeatures(degree=2) #다항회귀 차수 지정
X_train_poly =poly_features.fit_transform(X_train) # 2차 다항식으로 변환하여 학습
X_test_poly = poly_features.transform(np.array(X_test).reshape(-1,1))# 자료타입으로 인한 에러가 발생할 수 있음, 버전으로도 발생할 수 있음
#2차식으로 바꾼 데이터를 학습
poly_model =LinearRegression()
poly_model.fit(X_train_poly, y_train)
y_pred_poly = poly_model.predict(X_test_poly) #예측값이 출력 2차항으로
##2차 다항식 평가지표
##평가지표를 불러오기
mse_poly =mean_squared_error(y_test, y_pred_poly)
r2_poly = r2_score(y_test, y_pred_poly)## 단순선형회귀
print(mse_linear)
print(r2_linear)
# 2차 다항식으로
print(mse_poly)
print(r2_poly)
'''
0.7282634839897112
0.45589490363155005
0.7213852414555748
0.46103382230474643
'''
성능 면에서 2차 다항식 회귀가 조금 더 좋은 성능을 보였다.
poly_ols_model=sm.OLS(y_train, X_train_poly).fit()ols_model.summary()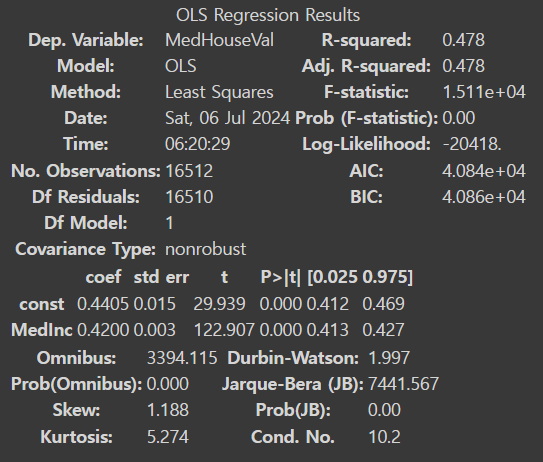
poly_ols_model.summary()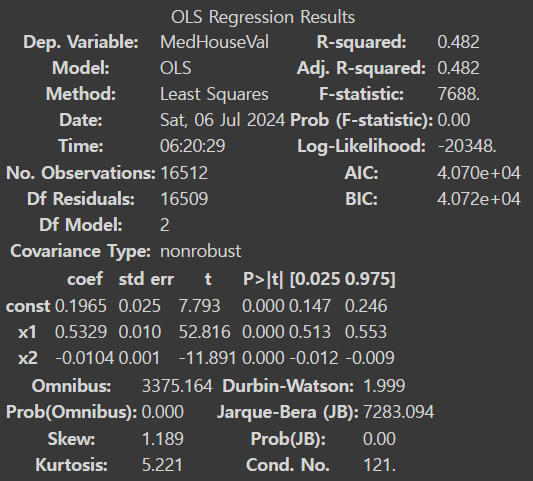
피처를 2개 활용하였을 때 성능 변화를 확인해본다.
#2개의 피처를 선택
#2개의 피처 기준은 피처셀렉션을 통해 선정하여 2개를 추가해서 다중회귀로 분석해 보자!
X=df[['MedInc','AveRooms']]
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.2, random_state=111)## 다중회귀학습
multiple_model =LinearRegression()
multiple_model.fit(X_train, y_train) # 독립변수가 2개 이상인 값이 들어가는 것
y_pred_multiple = multiple_model.predict(X_test) #예측값이 출력
## 다중회귀로 진행했을 때 , 2개의 피처 사용
mse_multiple =mean_squared_error(y_test, y_pred_multiple)
r2_multiple = r2_score(y_test, y_pred_multiple)print(mse_multiple)
print(r2_multiple)
## 단순선형회귀
print(mse_linear)
print(r2_linear)
# 2차 다항식으로
print(mse_poly)
print(r2_poly)
'''
0.7154473365884868
0.46547018959620234
0.7282634839897112
0.45589490363155005
0.7213852414555748
0.46103382230474643
'''
피처를 추가하면서 성능과 R값이 증가하였다. 하지만, 경우에 따라서 피처를 추가했을 때, 성능이 떨어질 수 있으며, 피처의 스케일링, 연속성을 판단하여 추가하는 것이 중요하다.
multiple_ols_model=sm.OLS(y_train, X_train).fit()
multiple_ols_model.summary()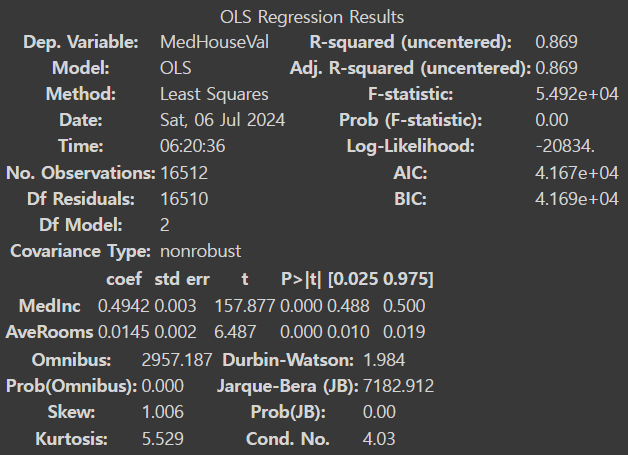
'B.D.A' 카테고리의 다른 글
| [BDA 데이터 분석 모델링반 (ML 1) 12회차] 로지스틱 회귀 (10) | 2024.07.24 |
|---|---|
| [BDA 데이터 분석 모델링반 (ML 1) 11회차] 라쏘 회귀, 릿지 회귀 (6) | 2024.07.17 |
| [BDA 데이터 분석 모델링반 (ML 1) 9회차] 선형회귀 응용 (4) | 2024.06.29 |
| [BDA 데이터 분석 모델링반 (ML 1) 8회차] 선형회귀 (5) | 2024.06.28 |
| [BDA 데이터 분석 모델링반 (ML 1) 7회차] RFM 분석 (7) | 2024.06.05 |




