[AAAI 2021] 3D Bin Packing with Constrained Deep Reinforcement Learning

본 연구는 3D BPP를 해결하기 위해 Actor-critic 구조를 가진 DRL을 활용하여 3D BPP 문제를 해결하는 연구이다.

논문 정보

Online 3D Bin Packing with Constrained Deep Reinforcement Learning

Papers with Code - Online 3D Bin Packing with Constrained Deep Reinforcement Learning

---

Abstract

Agent는 패킹해야 할 아이템의 제한된 정보를 토대로 아이템 배치는 순서 의존성과 물리적 안정성, 도착하면 즉시 패킹해야한다는 제약과 buffering과 readjusting는 불가능하다는 제약을 가진다.

이런 Online 3D-BPP를 CMDP(Constrained Markove decision process)로 정의한다.

 

Constrained Deep Reinforcement Learning (DRL)을 Actor-critic 구조에 따라 해결 방법을 제안한다.

특히, prediction-and-projection를 도입하여 에이전트는 배치 행동에 대한 가능성 마스크(feasibility mask)를 예측하고, 이후, 훈련 중에 배우가 출력하는 행동 확률을 마스크를 사용해 조정한다. 

 

이런 방법은 lookahead items, multi-bin packing, item re-orienting에 활용될 수 있다.

 

 

1. Introduction

빈팩킹 문제에서 최적의 배치는 모든 아이템을 최소한의 빈에 배치하며, 빈에 담긴 아이템의 총 무게는 빈의 용량 c를 초과하지 않도록 한다(Korte and Vygen 2012).

Fig 1: Online 3D-BPP, where the agent observes only a limited numbers of lookahead items (shaded in green), is widely useful in logistics, manufacture, warehousing etc.

 

택배는 주로 정육면체 모양이며, 이러한 택배를 표준 크기의 직사각형 빈에 집합적으로 패킹한다. 빈의 저장 공간 활용도를 최대화하면 재고 관리, 포장, 운송, 창고 보관 비용을 효과적으로 줄일 수 있다.

 

최신 기술력으로는 약 1,000개의 아이템을 포함한 큰 1D-BPP 인스턴스를 수십 분 이내에 정확하게 해결할 수 있으며(Delorme, lori, and Martello, 2016), 좋은 근사치를 밀리초 단위로 얻을 수 있다. 반면, 3D-BPP는 상대적으로 연구가 부족하여 휴리스틱 알고리즘에 의존하여 문제를 풀어야 한다(Crainic, Perboli, and Tadei, 2008; Karabulut and Inceoglu, 2004).

 

현재 3D-BPP는 모든 아이템의 정보가 미리 알려져 있다고 가정하며, 물리적 안정성을 고려하지 않고, 아이템을 다시 꺼내서 재배치하는 것을 허용한다(Martello, Pisinger, and Vigo, 2000).

 

그러나, 이는 현실과 거리가 멀고, 로봇은 앞에 들어올(테트리스와 유사하게) 몇 개의 아이템만 확인 가능하며, 아이템이 도착한 후 정해진 시간 내에 패킹해야 한다. 또한, 로봇이 빈에 이미 패킹된 아이템을 자주 unload하고 readjust하는 것은 비용이 많이 든다. 이런 제약은 3D-BPP를 복잡하게 만드는 요인이다.

 

문제 해결을 위해 3D-BPP를 위한 심층 강화 학습 알고리즘을 설계한다.

 

applicability를 최대화하는 목적함수로 설정하였고, 제약조건은 아이템 배치가 순서 의존성을 만족시킨다는 점과 불안정한 stacking을 유발하지 않도록 한다는 점, 아이템은 도착하자마자 즉시 패킹되며, 패킹된 이후 조정이 허용되지 않는다는 점을 포함하고 있다.

 

이를 위해 CMDP를 공식화하고, 정책 최적화를 위해 Actor-critic 프레임워크를 기반으로 한 접근 방식을 제안한다.

 

특히, prediction-and-projection를 도입하여 에이전트는 배치 행동에 대한 가능성 마스크(feasibility mask)를 예측하고, 이후, 훈련 중에 배우가 출력하는 행동 확률을 마스크를 사용해 조정한다.

 

 

2. Related Work

1D-BPP

1D-BPP는 조합 최적화 문제 중 하나이며, 대표적으로 다양한 무게를 가진 원하는 아이템을 생산하기 위해 빈을 자르는 문제인 절단 재고 문제(CSP)가 있다. NP-hard 문제로 알려져 있어 대부분의 기존 문헌은 좋은 휴리스틱 및 근사 알고리즘을 설계하고, 최악의 경우 성능 분석에 집중하고 있다.

 

예시로, NF(next fit algorithm)는 선형 시간 복잡도 $O(N)$을 가지며, 최악의 경우 성능 비율은 2이다. FF(first fit algorithm)는 아직 가득 차지 않은 이전 빈에 아이템을 패킹할 수 있게 하며 시간 복잡도는 $O(N\textrm{log}N)$ 이다. BF(best fit algorithm)은 가득 차지 않은 빈의 잔여 용량을 줄이는 것을 목표로 가진다.

 

모든 아이템이 사전에 정렬되면, Greedy 전략의 오프라인 버전이 생성되고, decreasing version(Martello 1990)으로 불린다.

 

2D- and 3D-BPP

1D와 2D/3D 패킹 문제의 주요 차이점은 패킹의 실현 가능성을 확인하는 것으로, 아이템을 빈 내부에 삽입할 수 있는지, 빈 크기 내에서 패킹되는지 여부를 결정하는 것이다.

보고된 시간 통계를 고려하면, 실제로 수천 개의 택배를 처리할 수 있는 3D-BPP를 정확하게 해결하는 것은 불가능하다. 따라서 근사 알고리즘을 활용하는 것이 좋다.

 

Hifi et al. (2010)은 문제에서 정수 제약을 완화하여 3D-BPP를 위한 혼합 선형 프로그래밍 알고리즘을 제안하였다.

Crainic et al. (2008)은 다가올 아이템을 극한 점으로 배치하여 빈의 사용되지 않은 공간을 더 잘 탐색하는 코너 포인트의 아이디어(Martello, Pisinger, and Vigo, 2000)를 개선했다.

 

휴리스틱 로컬 검색은 솔루션 집합에 대한 이웃 함수 내에서 탐색하여 기존의 패킹을 반복적으로 개선한다.

빠른 근사 알고리즘을 설계하는 데에는 guided local search, greedy search, tabu search 등 여러 가지 전략이 있다.

 

이에 반해, 유전 알고리즘은 전역적이고 무작위화된 탐색을 통해 솔루션을 도출한다.

 

Deep reinforcement learning (DRL)

DRL은 복잡한 행동 기술을 학습하고 고차원 원시 감각 상태 공간에서 어려운 제어 작업을 해결하는데 있어 성공을 거두었다.

 

기존 연구는 크게 on-policy와 off-policy로 나뉜다.

on-policy 알고리즘은 현재 정책에서 샘플링한 Agent-Environment 상호작용 데이터를 사용하여 정책을 최적화한다.

오래된 데이터를 재사용할 수 없다는 점에서 데이터 효율성은 떨어지지만, on-policy 데이터로 계산된 업데이트는 안정적인 최적화를 이끌어낸다.

 

본 연구에서는 Agent-Environment 상호작용 데이터를 얻기가 쉬워 데이터 효율성은 중요하지 않다.

따라서, on-policy actor-critic 프레임워크를 기초로 하여 방법을 설계했다.

 

RL for combinatorial optimization

조합 최적화를 위한 RL은 TSP에 초점을 맞춰 활성화되고 있다. (Bello et al. 2016)

RL pretraining과 active search를 결합하여 RL 기반 최적화가 NP-hard 조합 문제를 해결할 때 지도 학습 프레임워크를 능가한다.

 

이후, Hu et al. (2017)은 3D-BPP에 대한 DRL 솔루션을 제안하였다.

3. Method

Online 3D-BPP에서는 agent는 아이템의 크기에 대해 알지 못하고, 크기는 오직 즉시 도착하는 아이템 집합 만을 확인할 수 있으며,

도착한 아이템은 즉시 빈에 배치하고, 이후에 다시 배치하거나 조정할 수 없으며, 모든 아이템의 크기는 빈 크기의 절반 이하이다.

 

이런 문제를 해결하기 위해 Actor-critic 프레임워크 기반의 제약된 심층 강화 학습(DRL) 방법을 제안한다.

 

Fig 2: Left: The environment state of the agent includes the configuration of the bin (the grey boxes) and the size of the next item to be packed (green box). The bin configuration is parameterized as a height map H over a L × W grid. The feasibility mask M is a binary matrix of size L × W indicating the placement feasibility at each grid cell. The three dimensions of the next item are stored into a L × W × 3 tensor D. Right: The network architecture (the three losses other than the standard actor and critic losses are shown in red color).

 

 

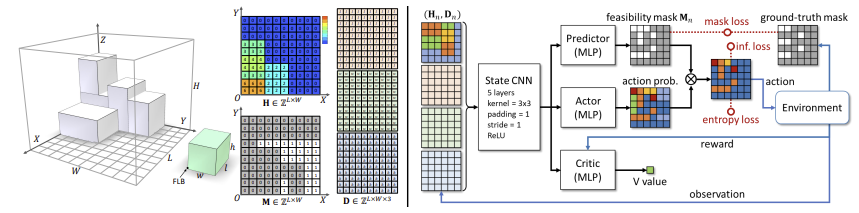
3.1. Problem statement and formulation

 

3D-BPP는 마르코프 결정 과정(MDP)로 공식화 할 수 있으며, $S$(상태 집합), $A$(행동 집합), $P$(상태 전이 확률), $R$(보상 함수)로 구성된다.

여기서 $P(s'|s,a)$는 상태 $s$에서 행동 $a$를 선택했을 때, 상태 $s'$으로 전이될 확률을 의미한다.

정책 $\pi$는 상태에서 행동으로의 확률적 매핑을 의미하며, $\pi(a|s)$는 상태 $s$에서 행동 $a$를 선택할 확률이다.

여기서 누적 보상인 $J(\pi)=E_{\tau\sim \pi}[\sum_{t=0}^{\infty}\gamma ^{t}R(s_t,a_t)]$를 최대화하는 정책 $\pi$를 찾고자 한다.

 

3D-BPP의 환경 상태는 빈의 현재 구성과 다음으로 배치될 아이템의 정보로 구성된다.

빈의 바닥 면적은 길이 $L$과 너비 $W$ 방향의 격자로 이산화하여 격자 셀에 쌓인 아이템의 높이를 기록한 height map $H_n$을 생성한다.

이때 $n$은 다음에 패킹될 아이템을 나타내며, 아이템 $n$의 크기는 $d_n = [l_n,w_n,h_n]^\top$로 정수형으로 주어진다.

아이템을 내려놓는 과정에서 현재 상태는 $s_n = \left\{ H_n, d_n, d_{n+1}, \cdots, d_{n+k-1} \right\}$ 로 표현한다. 

고려할 수 있는 선행 아이템의 수는 $k = |I_O|$로 표현하며, 고려하는 선행 아이템 수에 따라 BPP-$k$의 형태로 표현한다.

 

BPP-1

Agent는 front-left-bottom(FLB) 코너를 빈의 특정 격자 위치에 배치한다. 아이템 $n$을 내려놓는 위치는 $(x_n, y_n)$이며, 행동은 $a_n = x_n + L \cdot y_n \in A$으로 표현한다. 행동 후에는 높이 맵 $H_n$은 아이템 $n$이 차지하는 셀의 최대 높이에 $h_n$을 더하는 방식으로 업데이트 된다. 따라서, $H'_n(x,y) = h_\textrm{max}(x,y)+h_n$이다.

상태 전이는 $H = H'_n$ 이면, $P(H|H_n, a_n) = 1$이고, 그렇지 않으면 $P(H|H_n, a_n) = 0$이다.

 

빈에 아이템을 추가할 때에는 배치할 충분한 공간이 확보되어야 하며, 동시에 배치된 아이템이 물리적으로 안정적이어야 한다.

내려놓을 수 있는 위치가 가능하다고 간주되는 조건은 다음 3가지로 정한다.

1) 아이템의 바닥 면적 60% 이상이 다른 아이템에 의해 지지되며, 네 개의 바닥 모서리 모두 지지되는 경우

2) 바닥 면적의 80% 이상과 세 개의 바닥 모서리가 모두 지지되는 경우

3) 바닥 면적의 95% 이상이 지지되는 경우

이러한 가능성은 $L\times W$ 크기의 이진 행렬인 feasibility mask $M_n$으로 저장한다(Fig 2).

 

CMDP에서는 보조 비용 함수 $C$를 도입하여 비용을 매핑하고, 누적된 비용이 일정한 한계를 초과하지 않도록 한다.

$c_m: J_C(\pi)=E_{\tau\sim \pi}[\sum_{t=0}^{\infty}\gamma_C ^{t}C(s_t,a_t)]\leq c_m$

 

 

3.2. Network Architecture

Actor-critic framework with Kronecker-Factored Trust Region(ACKTR)를 활용하였다.

Actor와 critic를 함께 반복적으로 업데이트하고, Actor는 각 행동에서 나오는 정책 네트워크를 학습하고, critic는 state-value 네트워크를 학습한다.

실험을 통해 ACKTR과 같은 on-policy 방법이 SAC와 같은 off-policy보다 더 나은 성능을 보인다는 것을 확인하였다(Haarnoja et al 2018).

 

State input

CNN을 사용하여 원시 상태 벡터를 특징으로 인코딩하도록 설계하였다.

$d_n$을 three-channel tensor $D_n \in \mathbb{Z}^{L\times W\times 3}$로 확장하였고, $d_n$의 각 채널은 $L\times W$ 행렬로, 모든 요소가 각각 $l_n$, $w_n$, $h_n$ 값을 가진다. 결과적으로 현재 상태 $s_n = (H_n, D_n)$은 $L \times W \times 4$ 배열로 표현된다.

 

Reward

단순화된 단계별 보상을 정의한다. 현재 아이템들의 부피 점유율로, $r_n = 10\times \frac{l_n\cdot w_n \cdot h_n}{L\cdot W\cdot H}$이다.

현재 아이템을 배치할 수 없을 때, 보상은 0이 되며, 에피소드가 종료된다.

Feasibility mask를 사용하여 유효하지 않은 행동을 탐색하는 노력을 절약하고, 단계별 보상은 Agent가 가능한 한 많은 아이템을 배치하도록 유도한다.

 

Feasibility constraints

Feasibility constraints를 적용하기 위해 prediction-and-projection 메커니즘을 설계하였다.

먼저, MLP 모듈을 도입하여 feasibility mask $M_n$을 예측한다.

예측기는 현재 상태의 CNN 특징을 입력으로 받아 실제 mask를 감독 데이터로 사용하여 훈련한다.

다음으로, 예측된 마스크를 사용하여 행동의 확률을 조정한다.

 

이론적으로 위치 $(x,y)$가 아이템 $n$에 대해 가능하지 않는다면, $P(a_n = x + L \cdot y|s_n)$은 0으로 설정되어야 한다.

그러나, 실험을 통해 작은 양수를 도입하는 것이 더 좋은 결과를 낸다는 것을 확인했다.

 

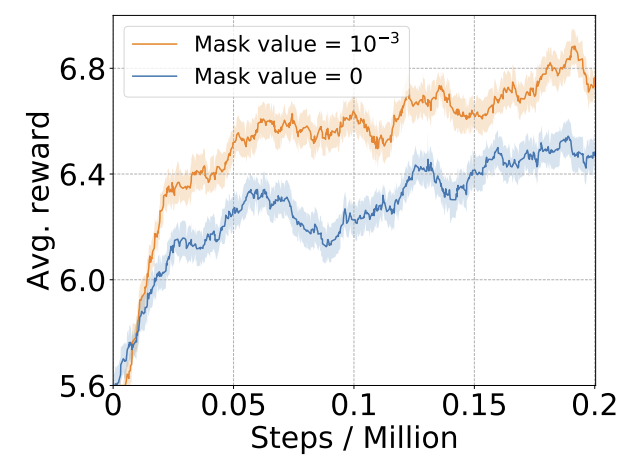
이는 유효하지 않은 행동에 강력한 패널티를 주면서 동시에 네트워크 훈련에 유리한 부드러운 변환을 제공한다.

유효하지 않은 행동을 억제하기 위해 유효하지 않은 로딩 위치에 합산 확률을 최소화하였다.

$E_\textrm{inf} = \sum P(a_n = x + L \cdot y|s_n), \forall (x,y)|M_n(x,y) = \epsilon$ 를 최종 손실 함수에 포함하여 훈련한다.

 

 

Loss function

손실 함수는 다음과 같다.

$$L = \alpha \cdot L_{actor} + \beta \cdot L_{critic} + \lambda \cdot L_{mask} + \omega \cdot E_{inf} - \psi \cdot E_{entropy}$$ 

$L_{actor}$ 와 $L_{critic}$ 는 actor와 critic를 훈련하기 위해 사용되는 손실 함수이다. $L_{mask}$ 는 마스크 예측에 대한 MSE 손실 함수이다.

Agent가 더 많은 로딩 위치를 탐색하도록 유도하기 위해 행동 엔트로피 손실 $E_{entropy} = \sum_{M_n(x,y)=1}^{}- P(a_n|s_n) \cdot \textrm{log}(P(a_n|s_n))$ 를 사용한다.

실험을 통해 가중치 값은 $\alpha = 1$, $\beta = \lambda = 0.5$, $\omega = \psi = 0.01$ 로 구하였다.

 

 

3.3. BPP-$k$ with $k = |I_O| > 1$

 

일반적인 경우 Agent는 $k > 1$ 개의 선행 아이템의 정보를 받는다.

이런 상황에서의 상태 시퀀스 $(d_n, \cdots, d_{n+k-1})$ 의 순차적 모델링을 사용하여 해결할 수 있다.

 

핵심 아이디어는 현재 아이템 $n$ 의 배치를 다음 $k-1$ 개의 아이템에 조건화하는 것이다.

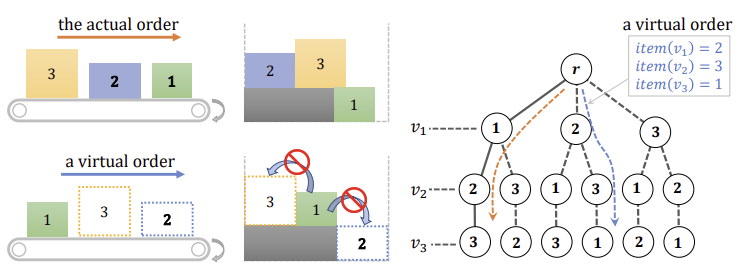
실제 배치는 도착 순서를 따르지만, 우리는 미래 아이템의 배치를 상상하여 높이 맵을 적절히 업데이트한다.

이런 가상 배치에서는 순서 의존성 제약을 만족하도록 해야 한다. 즉, 선행 아이템이 후속 아이템 위에 놓이지 않도록 해야 한다.

 

Monte Carlo permutation tree search

$(d_n, \cdots, d_{n+k-1})$ 시퀀스의 순열을 탐색하여 더 나은 행동 $a_n$을 찾는 탐색 기반 접근 방식을 채택한다.

순열 트리 탐색을 통해 수행되며, 트리의 각 경로는 가능성 있는 $k$ 개의 아이템 배치 순서를 나타낸다.

Fig 3: The permutation tree for Io = {1, 2, 3}. To find the best packing for item 1, our method explores different virtual placing orders satisfying the order dependence constraint, e.g., 1 cannot be placed on top of virtually placed 2 or 3

 

4. Experiments

프레임워크는 Intel Xeon Gold 5115 CPU @ 2.40 GHz, 64GB 메모리, 12GB 메모리의 Nvidia Titan V GPU에서 구현되었다.

DRL은 Pytorch에서 구현하였으며, 모델 훈련에는 10 x 10의 공간 해상도로 약 16시간이 걸렸다. BPP-1 모델의 테스트 시간은 10ms 미만이다.

 

Training and test set

 

실험에서는 $L = W = H = 10$, 64개의 크기가 사전 정의된 아이템을 사용하였다. 각 아이템의 크기는 빈 크기의 절반 이하로 설정하였다.

 

무작위로 $I$에서 아이템을 샘플링하여 시퀀스를 생성하는 RS를 만들었다.다만, 무작위 샘플링의 단점은 최적의 시퀀스를 알 수 없고, 성공적으로 패킹될 수 있는지 여부를 알 수 없기 때문에 패킹 성능을 측정하는 것은 어렵다.

 

이를 해결하기 위해 절단 재고(Gilmore and Gomory, 1961)를 사용하여 훈련 시퀀스를 생성하였다.이 방법을 통해 시퀀스가 완벽하게 패킹될 수 있으며, 빈으로 되돌릴 수 있음을 이해할 수 있다.

 

CUT-1 : 절단 후, 결과 아이템들을 FLB 좌표의 z축 좌표에 따라 시퀀스에 정렬한다. 두 아이템의 FLB 좌표가 동일한 z축 좌표를 가지고 있다면, 시퀀스에서의 순서는 무작위로 결정된다.

 

CUT-2 : 절단된 아이템들은 쌓이는 순서에 따라 정렬된다. 아이템은 그것을 지지하는 모든 아이템들이 시퀀스에 먼저 추가된 이후에만 추가될 수 있다.

 

RS, CUT-1, CUT-2 각각에 대해 2,000개의 시퀀스를 생성하였다.

 

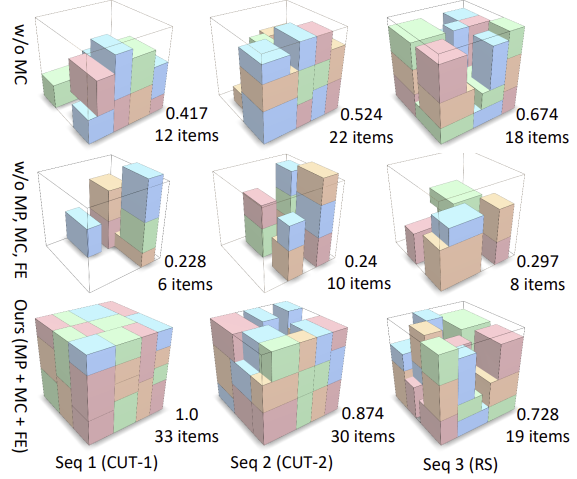
Ablation study

Table 1: This ablation study compares the space utilization and the total number of packed items with different combinations of MP, MC and FE, on the CUT-2 dataset.

 

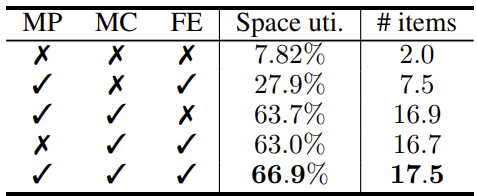
MP(Mask Prediction) : 강화 학습 Agent가 물체를 빈에 배치할 때 가능한 위치를 예측하는 메커니즘이다.

MC(Mask Constraint) : 마스크 예측을 강화하는 제약 조건, 마스크 제약은 Agent가 물체를 물리적으로 불가능한 위치에 배치하는 것을 방지하기 위해, 배치 가능한 위치만 선택하도록 강제하는 역할을 한다.

FE(Feasibility-based Entropy) : Agent가 다양한 행동을 시도하도록 유도하는 메커니즘으로, 배치할 수 있는 가능한 위치들 간의 행동 확률 분포를 넓게 유지하여 Agent가 여러 가지 행동을 시도하도록 한다. 

Fig 4. Packing results in the ablation study. The numbers beside each bin are space uti. and # items

 

Height parameterization

2D 높이 맵(HM)을 사용한 환경 매개 변수화를 2가지 1D 대안과 비교하였을 때, 더 효과적임을 확인하였다.

 

1D 대안으로는 HV(Height Vector)와 ISV(Item Sequence Vector)가 있다.

HV는 $H$의 열을 쌓아 만든 $L \cdot W$ 차원의 벡터이다.

ISV는 빈에 현재 패킹된 모든 아이템의 정보를 나열하는 벡터로, 각 패킹된 아이템은 FLB의 x,y,z 좌표와 아이템 크기에 해당하는 6개의 매개 변수를 가진다.

Fig 5: HM shows a clear advantage over vector-based height parameterizations (HV and ISV).

 

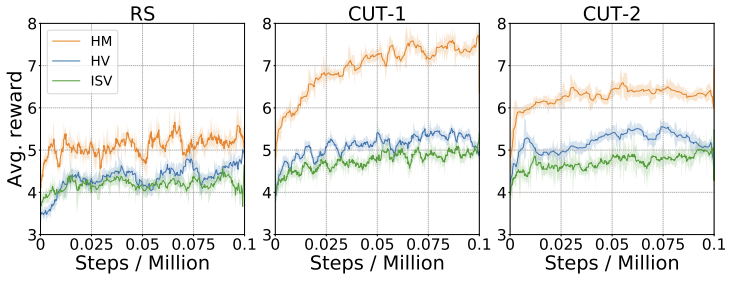
CUT-1에서의 테스트 결과, HM은 공간 활용도에서 16%~19% 정도 더 높은 성능을 보였으며, HV와 ISV보다 각각 4.3개, 5개의 더 많은 아이템을 패킹하였다.

 

Constraint vs. reward

Fig 6. Comparison to DRL with reward tuning. Our method obtains much better space utilization.

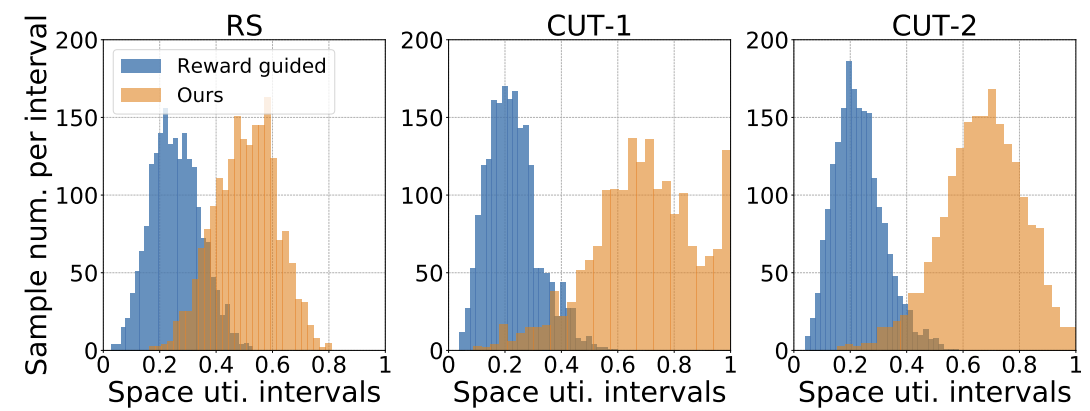
DRL 훈련에서는 low-profile 행동을 억제하기 위해 보상함수를 조정하지만, 연구에서는 mask를 예측하여 유효하지 않은 행동을 학습하는 방법을 활용한다. 그 결과, Constraint-based DRL은 잘못된 행동을 거의 예측하지 않으며, 더 나은 공간 활용도를 보여준다.

 

Scalability of BPP-$k$

Fig 7. (a): Our permutation based MCTS maintains good time efficiency as the number of lookahead items increases. (b): The performance of our MCTS based BPP-k model achieves similar performance (avg. space utility) as the brute-force search over permutation tree. (c): The distribution of space utilization using boundary rule (Heu.), human intelligence (Hum.), and our BPP-1 method (Ours).

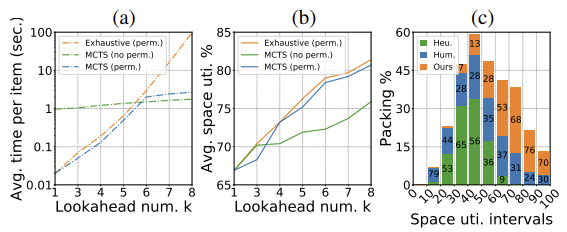
$k$개의 선행 아이템에 대한 모든 $k!$ 순열을 순차적으로 탐색하는 브루트 포스 순열 탐색과 본 연구에서 활용한 MCTS(Monte Carlo Tree Search)를 활용한 패킹 전략을 비교하였다. 그 결과, MCTS 기반 순열 트리 탐색이 최적화된 결과를 제공하면서 동시에 브루트 포스 탐색보다 효율적임을 확인하였다.

 

Extension to different 3D-BPP variants

Table 2. Multi-bin packing tested with the CUT-2 dataset.

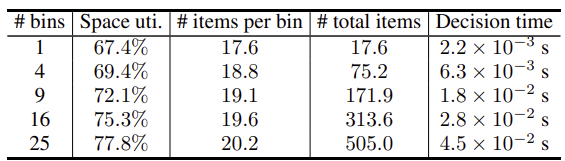
본 연구는 다중 빈 사용 문제, 아이템 재배치와 같은 3D bin-packing 변형 문제를 쉽게 처리할 수 있다. 다중 빈 3D-BPP를 실현하기 위해 총 빈수에 맞는 여러 BPP-1 인스턴스를 초기화한다. 아이템이 도착하면, 해당 아이템을 배치했을 때 critic 가치 감소가 가장 적은 빈에 패킹한다. 다중 빈 패킹 테스트 결과는 Table 2에서 확인할 수 있다.

 

아이템의 수평축 정렬만 허용하므로, 각 아이템은 두 가지 가능한 방향을 가질 수 있으며, 각 아이템에 대해 두 개의 가능성 마스크를 생성하며, 행동 공간도 두 배로 확장된다. 네트워크는 확장된 행동 공간에서 행동을 하도록 훈련되며, RS 데이터 세트에서의 테스트 결과, 재배치를 허용할 경우 공간 활용도가 11.6% 증가하고, 평균 패킹된 아이템 수가 3개 증가하였다.

 

Comparison with non-learning methods

Table 3: Comparison with three baselines including both online and offline approaches.

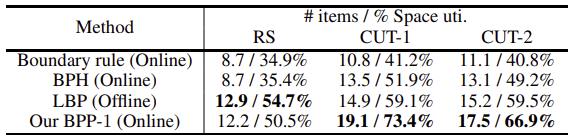
기존 연구는 대부분 오프라인(전체 아이템 시퀀스가 사전에 알려진) BPP에 집중하며, 비학습 방법을 채택한다.

 

본 연구에서는 사용할 수 있는 2가지 대표적인 방법과 성능을 비교하였다.

첫 번째는 휴리스틱 기반 온라인 접근법인 BPH(Ha et al., 2017)로, Agent가 $k$개의 선행 아이템 중 최적의 아이템을 선택할 수 있게 한다.

두 번째는 오프라인 LBP(Martello, Pisinger, and Vigo, 2000)으로, 경계 규칙 방법이라는 휴리스틱 기반의 기준선을 설계하였다. 이 방법은 새로운 아이템을 기존에 패킹된 아이템 옆에 배치하고, 패킹 부피를 최대한 규칙적으로 유지하려고 하는 인간의 행동을 모방한다.

 

Table 3에서 연구에서 활용한 방법은 모든 벤치마크에서 기존 온라인 방법보다 우수한 성능을 보였으며, 심지어 오프라인 접근법보다 더 좋은 성능을 보였다.

Fig 8. Comparison with the online BPH method (Ha et al. 2017) on BPP-k. Note that BPH allows lookahead item reordering while ours does not.

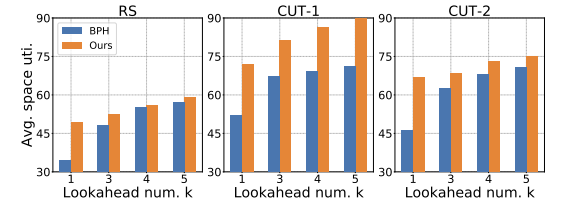
Fig 8에서는 연구에서 활용한 방법이 $k$개의 선행 아이템 수가 증가해도 온라인 BPH보다 일관되게 좋은 성능을 보여주었다.

 

추가로, 실제 로봇을 활용하여 50개의 무작위 아이템 시퀀스에서 본 연구의 방법은 평균적으로 66.3%의 공간 활용도를 달성하였으며, 이는 경계 규칙(39.2%)와 온라인 BPH(43.2%)보다 높은 성능을 보였다.

 

Our method vs. human intelligence

50명의 사용자가 수동으로 아이템을 패킹하는 것과 본 연구 방법을 비교하였다.

본 연구 방법은 일반적으로 인간 플레이어보다 더 나은 성능을 발휘하였다(1339번의 AI 승리, 406번의 인간 승리, 98번의 무승부).

본 연구 결과는 1,851개의 게임에서 평균적으로 68.9%의 공간 활용도를 달성했으며, 인간은 52.1%를 달성했다.

 

5. Conclusion

온라인 3D-BPP를 CMDP(Constrained Markov decision process)로 공식화하고, 제약된 DRL을 사용하여 해결하였다.

Actor-critic 구조를 사용하여 복잡한 제약 조건이 있는 상태에서 정책 최적화를 달성하고, 높이 맵 기반의 빈 표현과 행동 가능성 예측에 활용하였다.

다수의 선행 아이템이 주어진 상황에서 최적의 행동을 찾기 위해 MCTS(Monte Carlo Tree Search)를 사용하여 선행 아이템의 순열을 탐색하였다.

 

향후 연구에서는 선행 아이템의 순서 의존성 제약을 완화하는 방향과 불규칙한 형태의 아이템을 패킹하는 방법을 학습하는 방향으로 발전시켜볼 수 있다.