[ICML 2024] DISTILLM: Towards Streamlined Distillation for Large Language Models

본 논문 리뷰는 개인적인 학습 내용을 바탕으로 작성된 것으로, 일부 내용에 오류가 있을 수 있습니다.

 

논문 정보

Ko, J., Kim, S., Chen, T., & Yun, S. Y. (2024). Distillm: Towards streamlined distillation for large language models. arXiv preprint arXiv:2402.03898.

DistiLLM: Towards Streamlined Distillation for Large Language Models

---

Abstract

KD(Knowledge distillation) : teacher model을 더 작은 student model로 축소시키는 과정에서 모델을 어느 정도 보존하면서 inference cost와 memory footprint를 줄이는 과정이다.

 

다만, *auto regressive sequence model에서 표준화된 목적 함수를 놓치고 있으며, training-inference mismatches를 해결하기 위해 SGO(student generated outputs)를 사용하면서 계산 비용이 크게 증가했다.

*Auto Regressive Sequence Model : 시퀀스 이전 값으로 다음 성분을 자동으로 예측하는 ML 클래스

 

이런 문제점을 해결하기 위해 다음의 차별점을 가진 DISTILLM을 제안한다.

(1) skew *KLD(Kullback-Leibler divergence) loss를 사용한다.

(2) adaptive off-policy 접근방법을 활용한다.

*KLD : teacher model과 student model의 두 확률분포의 차이를 계산하는 함수

 

그 결과, DISTILLM은 기존의 KD 방법에 비해 최대 4.3배의 속도 향상을 보였다.

 

Introduction

LLM 성능을 유지하면서 매개변수를 줄이는 것이 중요해지고, teacher model의 경량화로 student model을 제안하는 것이 중요하다.

 

기존의 KLD에는 두가지 문제점이 있다:

Mode Averaging or Mode Collapse : student model이 지나치게 매끄러워 teacher model의 분포를 포착하지 못하거나 확률이 높은 분포에 집중하게 되면서 최적이 아닌 결과를 가져올 수 있다(Wen et al., 2023; Gu et al., 2024).

Bias problem : 훈련 중에 관찰된 시퀀스와 student model이 생성한 시퀀스 사이에 분포 불일치가 발생할 수 있다(Arora et al., 2022).

 

이를 해결하기 위한 방법으로 student-generated output(SGO, Lin et al. 2020; Agarwal et al. 2024)를 활용하는 방법도 있지만, 지속적인 SGO 생성은 효율성이 떨어질 수밖에 없다.

 

Contributions.

DISTILLM : a novel skew KLD loss + an adaptive off-policy approach

skew KLD : 안정적인 기울기와 최소 근사 오차에 최적화된 새로운 목적함수 제안

Adaptive off-policy approach : SGO를 적응적이고 효율적으로 활용하기 위한 off-policy 접근 모듈을 제안

Advanced performance and efficiency : DISTILLM은 최근 KD 기술에 비해 2.5~4.3x 훈련 속도 향상을 달성한다.

 

Background

KD for Auto-regressive Generative LMs

KD는 주어진 소스 및 타겟 시퀀스 쌍 $(x, y)$에 대해 교사 모델 $p(y|x)$와 매개변수화된 학생 모델 $q_{\theta }(y|x)$의 분포 간의 차이를 최소화한다. 이때 훈련 데이터 쌍 $(x, y)$은 고정된 실제 데이터셋에서 샘플링하거나 교사 모델이 생성한 출력으로 이루어진다. 손실 함수는 간단하고 계산이 용이하다는 장점을 가진 KLD를 많이 사용한다.

 

$$D_{KL}(p, q_\theta) = \mathbb{E}_{X}\mathbb{E}_{Y \sim p(\cdot |X)}[\textrm{log}\frac{p(Y|X)}{q_{\theta}(Y|X)}]$$

 

$D_{KL}$은 교사 모델 분포 $p$와 학생 모델 분포 $q_\theta$ 간의 KLD이다. 이는 학생 모델이 교사 모델의 분포를 얼마나 잘 따라가고 있는지를 전체 데이터셋에 대해 두 모델의 분포 차이를 평균적으로 측정한다.

 

$$​\approx \frac{1}{|D|}\sum_{(X,Y)\in D}^{}p(Y|X)\textrm{log}\frac{p(Y|X)}{q_{\theta}(Y|X)}$$

 

고정된 데이터셋 $D$에서 샘플링된 각 시퀀스 쌍 $(x, y)$에 대해 KLD를 근사화하여 계산하는 방법을 제시하고,

$p(Y|X)\textrm{log}\frac{p(Y|X)}{q_{\theta}(Y|X)}$ 값을 모든 데이터에 대해 평균하여, 교사 모델과 학생 모델 간의 차이를 구한다.

 

$$= \frac{1}{|D|}\sum_{x\in D_X}^{}\sum_{t=1}^{|y|}\sum_{y_t\in V}^{}p(y_t|y_{<t},x)\textrm{log}\frac{p(y_t|y_{<t}, X)}{q_{\theta}(y_t|y_{<t},X)} $$

 

$V$는 어휘 집합이고, $y_{<t}$는 시퀀스의 이전 토큰들로 이루어진 부분 시퀀스이다. 이 수식은 토큰 레벨에서 KLD를 계산하여, 교사 모델이 각 시점에서 특정 토큰을 생성할 확률과 학생 모델이 같은 토큰을 생성할 확률 간의 차이를 측정한다. 이처럼 시퀀스 전체를 개별 토큰 단위로 분해하여 계산하는 방식을 통해 KLD를 효율적으로 사용할 수 있다.

 

KLD는 계산이 용이하고, 토큰 수준으로 분해하여 시퀀스 레벨을 쉽게 최적화할 수 있다는 장점이 있다.

 

 

Pitfalls of Existing Distillation

 

Limitation of objective functions.

KLD 목적 함수는 비대칭적 특성으로 학생 모델로 하여금 교사 모델 분포의 전체 지원 집합을 덮도록 강요하는 경우가 있다.

교사 분포에서 특정 데이터 포인트는 높은 확률 값을 가지지만, 학생 분포에서는 그 데이터 포인트에 대해 거의 0에 가까운 확률을 할당하는 상황이 발생할 수 있다.

학생 모델은 교사의 분포 전체를 덮으려 하면서 지나치게 부드러운 분포를 학습하게 되는 Mode Averaging Problem이 발생할 수 있다. 이러한 문제로 인해 학생 모델이 불필요하게 평탄한 분포를 학습하게 되며, 이는 모델의 성능에 부정적인 영향을 미칠 수 있다.

 

Mode Averaging Problem : KLD는 비대칭적이기 때문에, 학생 모델은 교사 모델 분포의 모든 가능성을 덮으려고 시도하게 되고, 이 과정에서 특정 데이터 포인트에 대해 교사 모델은 높은 확률을 할당하지만, 학생 모델은 모든 가능한 출력을 평탄하게 다루려다 보니 확률이 분산되고 고르게 나눠지는 현상이 발생한다.

 

이를 해결하기 위해 중간 값을 조절하는 보간 파라미터 $\beta$를 도입한다.

 

RKLD(Gu et al. 2024; Agarwal et al. 2024)

$$D_{RKL}(p, q_{\theta}) := D_{KL}(q_{\theta}, p)$$

 

JSD(Agarwal et al., 2024)

$$D^{\beta}_{JSD}(p, q_{\theta}):= \beta D_{KL}(p, \beta p + (1-\beta)q_{\theta}) + (1-\beta)D_{KL}(q_{\theta}, \beta p + (1-\beta)q_{\theta})$$

 

$D_{KL}(p, \beta p + (1-\beta)q_{\theta})$ : 교사 모델 분포 $p$와 $\beta$로 조절된 혼합 분포 사이의 KLD

$D_{KL}(q_{\theta}, \beta p + (1-\beta)q_{\theta})$ : 학생 모델 분포 $q_{\theta}$와 $\beta$로 조절된 혼합 분포 사이의 KLD

 

이러한 접근법들은 자동회귀 언어 모델에서 좋은 성공을 거두었지만, 체계적인 연구가 필요하며, 충분한 근거를 찾아야 한다.

 

 

Limitations of utilizing SGO.

KD 기법은 훈련에 사용되는 고정 데이터셋과 학생 모델이 추론 과정에서 생성하는 데이터 간의 불일치 문제를 가지고 있다. 훈련 시에는 고정된 데이터셋으로 학생 모델을 학습하지만, 추론 시에는 학생 모델이 스스로 출력을 생성하게 되면서 학생 모델이 실제 추론 환경에서 제대로 작동하지 않는 training-inference mismatch 문제가 발생할 수 있다.

최근 연구에서는 학생 모델이 SGO를 생성하도록 유도하고, 이에 대해 교사 모델의 피드백을 받아 학습하는 방식을 제안하였고, 스스로 생성한 익숙한 데이터를 기반으로 학습할 수 있도록 하여, 추론 환경과의 불일치를 줄이는데 도움을 주었다.

 

이런 SGO 기반 학습 방식은 LLM의 KD 성능을 크게 개선하였고, 학생 모델이 실제 추론 환경에서 직면하게 될 데이터를 스스로 생성하고 학습하여 훈련과 추론 간의 차이를 줄이고, 보다 일관된 성능을 얻을 수 있게 되었다.

 

 

GPT-2 학생 모델이 생성한 출력과 GPT-2 XL 교사 모델이 검증한 손실 값의 예시를 보여준다. 이 그림에서 교사 모델과 학생 모델 분포 불일치를 확인할 수 있다. 첫 번째 질문은 올바른 답변을 통해 손실 값이 낮은 상황이며, 두 번째 질문은 틀린 답변이지만, 짧은 길이로 인해 교사 모델이 낮은 손실 값을 할당하였다. 세 번째 질문은 올바른 답변이지만, 긴 길이로 인해 높은 손실 값을 부여하였다.

교사 모델이 학생의 SGO와 일치하지 않는 타깃 분포를 가지고 있다면, 잘못된 방향으로 학생 모델을 학습하게 만들 수 있다.

 

 

왼쪽 그래프는 SGO 최대 응답 길이에 따른 실행시간(계산 비용)을 표현한 그래프이며, 오른쪽 그래프는 교사, 학생 모델 크기의 쌍에 따른 정규화된 실행 시간이다. 각 그래프별 파란 부분은 SGO 생성에 소요되는 시간, 노란색은 학생 모델의 순방향 전파 시간, 초록색은 교사 모델의 순방향 전파 시간(정확한 정답 분포와 목표를 출력하는 과정), 빨간색은 학생 모델의 역방향 전파 시간(학생과 교사 모델의 출력 간의 차이를 바탕으로 파라미터 업데이트)이다. 매 학습이 반복될 때마다 SGO를 생성하는 것은 계산 효율성 측면에서 비효율적이다. SGO의 최대 시퀀스 길이와 모델 크기에 관계없이, SGO 생성은 전체 학습 시간의 최대 80%까지 차지한다.

 

이를 해결하는 접근법으로 MiniLLM(Gu et al., 2024)은 교사와 학생의 분포를 혼합하여 모델 간의 분포 불일치 문제를 완화하고자 했지만, 이는 교사 모델이 필요하기 때문에 계산 비용이 증가하는 단점이 있다.

DISTILLM은 훈련-추론 불일치 문제를 줄이면서 노이즈 피드백으로 인한 성능 저하를 방지하는 적응형 접근 방식을 제안한다.

 

 

DISTILLM

Skew KLD

기존 목적 함수의 한계를 보완하기 위해 설계된 손실 함수로, 최적화 안정성과 일반화 성능을 향상시킨다.

기존의 KLD에서 발생하는 한계를 극복하기 위해 teacher 모델이 분포 $p$와 학생 모델의 분포 $q_\theta$ 사이의 KLD를 두 분포의 혼합 분포인 $\alpha p + (1-\alpha)q_\theta$와 비교하는 방식으로 정의한다.

$$D_{SKL}^{(\alpha)}(p, q_\theta) = D_{KL}(p, \alpha p + (1-\alpha)q_\theta)$$

 

Skew Reverse KLD(SRKL)은 학생 모델 분포 $q_\theta$와 혼합 분포 $(1-\alpha)p + \alpha q_\theta $ 사이에 KLD로 정의한다.$$D_{SRKL}^{(\alpha)}(p, q_\theta) = D_{KL}(q_\theta, (1-\alpha)p + \alpha q_\theta)$$

 

Skew KLD와 SRKL은 다른 손실 함수보다 stable gradient와 smaller approximation error를 제공한다.

 

 

Stable gradient

기존 KLD에 대한 gradient는 다음과 같이 정의한다.

 

해당 gradient는 모델 확률의 negative gradient를 계산하며, 값이 낮을수록 가중치가 커진다.

$r_{p,q_\theta}$는 두 분포 $p$와 $q_\theta$의 비율인 $p(y|x)/q_\theta (y|x)$이다.

만약 $q_\theta (y|x) \approx 0$일 경우, gradient의 크기가 과도하게 커져 훈련 과정을 불안정하게 만든다.

 

Skew KLD의 gradient는 다음과 같이 정의된다.

 

$\tilde{q}_\theta (y|x)$는 혼합 분포로 다음으로 나타내며,

$$\tilde{q}_\theta (y|x) = \alpha p(y|x) + (1-\alpha)q_\theta(y|x)$$

 

SKL은 $(1-\alpha)$라는 추가 계수를 포함하며, $p$와 $q_\theta$의 혼합 분포를 사용하기 때문에 $r_{p, \tilde{q}_\theta}$가 0에 가까워지는 것을 방지한다. 따라서, SKL은 KLD에 비해 more stable gradient를 제공한다.

 

RKLD와 SRKL은 각각 다음과 같이 정의된다.

 

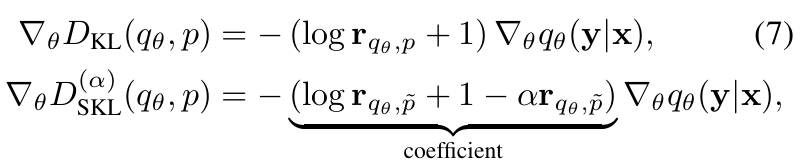
$\tilde{p} (y|x)$는 다음과 같은 혼합 분포이다.

$$\tilde{p}(y|x) = (1-\alpha)p(y|x) + \alpha q_\theta (y|x)$$

 

아래 Figure 3(a), (b)를 통해 $\alpha$가 커지면, SKL과 SRKL에서 계수의 효과가 작아질 수 있어 gradient의 안정성을 보장할 수 있다.

 

SKL과 SRKL은 $q_\theta (y|x) \approx 0$ 인 경우에도 gradient의 크기가 급격히 커지지 않도록 설계되어 있어 훈련 과정에서 불안정성을 줄이고, 더 빠르고 안정적인 학습을 가능하게 한다.

 

 

Small approximation error

SKL은 Bounded L2 norm으로 학습 데이터에서 계산한 값과 실제 값 간의 차이가 크지 않도록 보장하며 제한된 오차로 모델을 더 효율적으로 학습할 수 있으며, 전체 데이터 분포를 잘 반영할 수 있다.

 

$\alpha$가 클수록 $c_{1}(\alpha)$가 작아지고, 전체 L2 norm 상한이 낮아진다. 이는 Skew KLD 추정치가 실제 값과 더 가깝다는 의미를 가진다.

샘플 수 $n$이 증가하면 오차가 급격히 감소하여 더 많은 데이터로 학습할수록 안정성이 증가한다.

Figure 3(c)에서 $\alpha$ - S(R)KL가 KLD보다 미니배치와 이동 평균 간의 오차를 더 효과적으로 줄인다.

 

 

gradient 계수인 $(1-\alpha)$의 역수를 고려한 새로운 L2 norm 상한을 제안하였다.

JSD(Jensen-Shannon Divergence)는 두 분포의 skew 값을 동시에 조정할 수 없지만, S(R)KL은 $\alpha$ 값을 통해 조정할 수 있다.

$\alpha$ 값은 gradient와 L2 norm의 균형에 직접적인 영향을 미치며, $\alpha$가 작아지면, gradient의 크기는 커지지만, L2 norm은 감소한다.

따라서, $\alpha$의 적절한 선택이 중요하며, 실험에서는 값을 0.1로 했을 때, KLD, RKLD, JSD보다 우수한 결과를 제공하는 것을 확인하였다.

 

 

 

Adaptive Off-policy Approach

 

기존 SGO의 활용에서는 Noisy Feedback(Teacher model이 SGO를 이해하지 못해 발생하는 noisy 문제), Training Time Increase(모든 훈련에서 SGO를 사용하면 훈련 시간이 5.5배 증가할 수 있으며, 성능이 저하되는 문제) 문제점을 가지고 있다.

이를 해결하기 위해 Adaptive SGO scheduler와 효율적인 Off-Policy 전략을 제안하였다.

 

Adaptive SGO scheduler

SGO 활용 확률을 $\phi$로 정의했을 때, 기존 방법은 $\phi$를 일정하게 유지하는 방식으로, 이 방법은 Noisy Feedback의 위험을 증가시켜, 학생 모델의 학습 성능에 악영향을 줄 수 있다. 이를 해결하기 위해 $\phi$ 값을 낮게 시작하여 훈련 과정 중 모델의 검증 손실(validation loss)을 기반으로 점진적으로 $\phi$를 증가시킨다. 

검증 손실이 증가하면 $\phi$를 증가시켜 더 많은 SGO를 활용하도록 조정한다.

 

Off-policy approach for sample efficiency

기존의 On-policy 접근법은 새로운 데이터를 지속적으로 요구하여 자원 소모가 크다. 이를 해결하기 위해 Replay Buffer를 도입하여 과거에 생성된 SGO를 저장하여 재활용한다.

Replay Buffer의 작동 방식은 SGO를 확률 $\lambda_R$로 Replay Buffer $D_R$에 저장한다. 이후, 무작위로 샘플을 선택하여 학습에 활용하고, Buffer의 용량이 가득 차면 가장 오래된 데이터를 새로운 데이터로 교체한다.

Replay Ratio는 현재 학습 단계에서 얼마나 많은 SGO를 재활용할지를 결정하며, 다음과 같이 정의한다.

 

t는 현재 학습 반복 단계, T는 총 학습 반복 단계로 초기에 Replay Ratio 값은 크며, 학습 후반부로 갈수록 감소한다.

초기에는 학생 모델의 매개변수 변화가 크기 때문에 노이즈를 줄이기 위해 SGO 재활용 비율을 높게 설정하고, 후기에는 모델이 수렴하기 때문에 재활용 비율을 낮춰준다.

이런 Off-Policy 전략은 오류 감소와 샘플 효율성 간의 균형을 효과적으로 맞춰준다.

 

Synergy with SKL

SKL과 SRKL은 초기 학습 단계에서 빠른 수렴 속도를 가지고 있어 Off-Policy 접근법과 효과적으로 결합하며, Off-Policy 전략의 단점이 높은 편향 문제를 피하면서 효과적으로 초기 학습 성능을 끌어올릴 수 있다. 기존의 다른 접근법과 비교했을 때, 성능 저하가 없음을 확인하였다.

SKL과 Off-Policy 접근법의 결합은 학습 시간을 단축하면서도 높은 성능을 유지할 수 있는 효과적인 전략이다.

 

Experiments

DISTILLM의 성능을 Task-Agnostic Instruction-Following, Text Summarization, Machine translation으로 평가했다.

DISTILLM의 초기 설정은 $\phi = 0$, Replay Buffer의 크기는 1000, SKRL의 $\alpha = 0.1$로 설정하였다.

 

다음의 기존 KD 방법론과 DISTILLM을 비교하였다.

Supervised Fine-Tuning (SFT) : 고정된 데이터셋에서 학생 모델을 직접 Fine-Tuning 하는 방식

KD : 고정된 데이터셋에서 KLD를 사용하여 학습하는 방식

SeqKD : 교사 모델이 생성한 출력을 활용하여 SFT를 수행하는 방식

ImitKD : SGO에 대해 KLD를 적용하는 방식

MiniLLM : SGO에 대해 Policy Gradient를 적용하는 방식

GKD : SGO와 고정 데이터셋의 혼합에 대해 JSD를 적용하는 방식

 

그 결과, 고정된 데이터셋만을 사용하는 SFT, KD보다 유연하고 효율적이며, SeqKD, ImitKD, MiniLLM과 비교했을 때, SGO와 고정 데이터셋의 조화를 더 잘 활용하며, GKD와 비교해 학습 안정성과 성능을 높였다.

 

Task-Agnostic Instruction-Following

 

Implementation details

학습 데이터는 Databricks-dolly-15k 데이터셋에서 구성하여 14000개의 샘플은 학습에 사용되고, 나머지 500개는 검증 및 테스트에 사용하였다.

학습된 모델은 Dolly Evaluation, Self-Instruct, Vicuna Evaluation, Super-Natural Instructions, Unnatural Instruction에서 평가하였으며, OpenWebText 데이터셋을 사용하여 Language Modeling Loss를 추가로 적용하였다.

평가 지표로는 ROUGE-L(텍스트 생성의 유사도 측정), GPT-4 Feedback(GPT-4를 이용한 피드백 점수)를 사용하였다.

 

Main Results

DISTILLM은 다양한 교사-학생 조합과 평가 지표에서 최신 방법론을 능가하는 성능을 보였다. 특히, GKD와 MiniLLM은 최근 SGO를 활용했을 때, 소형 학생 모델에서 성능 저하를 보였지만, DISTILLM은 단점을 극복하며 일관된 성능을 발휘하였다.

대형 LLM에서 LoRA(Low-Rank Adaptation) 기술을 사용하여 대형 모델에 대해 DISTILLM을 평가한 결과, DISTILLM 방법이 다른 방법론보다 좋은 성능을 보였으며, 학습 시간 면에서는 약 3~7배 정도 효율적인 결과를 얻었다.

 

Text Summarization and Machine Translation

Text Summarization에서 사용한 데이터셋은 SAMSum(대화 요약 데이터셋)이며, T5-XL v1.1 교사모델과 T5-Base/Small v1.1 학생모델을 사용하였고, ROUGE-L(텍스트 요약의 품질 평가)를 평가 지표롤 사용하였다. Machine Translation에서는 IWSLT 2017(국제 워크샵에서 제공하는 기계 번역 데이터셋) 데이터셋과 mT5-XL 교사 모델과 mT5-Base/Small v1.1 학생 모델, 평가지표로는 BLEU(번역 품질 평가)를 사용하였다.

 

DISTILLM은 다른 방법론보다 전반적으로 우수한 성능을 보였지만, 단일 작업에서는 성능 차이가 크지 않았다.

목적함수와 SGO 사용의 효과는 작업에 따라 달라질 수 있다.

하지만, DISTILLM은 작업 간 차이에도 불구하고, SGO 스케줄러와 Skew Divergence를 활용하여 모든 작업에서 일관된 우수한 성능을 보였다.

 

 

추가적으로 ROUGE-L 점수를 $\alpha$ 값에 따라 비교한 결과, DISTILLM은 다양한 작업(Dolly Eval, Self-Instruct, Super-Natural)에서 $\alpha$ 값 변화에도 안정적으로 높은 성능을 유지하였다.

 

Analysis and Discussion

Effect of Skew Divergence

SKL과 SRKL은 기존 손실 함수(KLD, RKLD< JSD)보다 일관되게 높은 성능을 보였으며, Figure 6에 따르면, SKL과 SRKL은 학습 초기 단계부터 높은 ROUGE-L 점수를 달성하였다.

 

Effect of Adaptive Off-policy Approach

Adaptive Off-policy 방식을 On-policy 접근법과 Mixed Strategy(50% On-policy + 고정된 데이터셋) 방식으로 비교한 결과 노이즈 피드백과 훈련-추론 불일치 문제를 완화하였으며, SKL을 적용하였을 때, 모든 데이터셋에서 더 높은 성능을 보였으며, 학습 속도가 On-Policy와 Mixed Strategy 대비 2.2배에서 3.4배 더 빨랐다.

 

Additional Ablation Studies on DISTILLM

 

Skew values

$\alpha$가 모두 0.1일 때, SKL과 SRKL에서 가장 우수한 성능을 보이며, 0.1보다 커질 경우, SKL, SRKL 모두 성능 저하가 발생한다.

 

Combining off-policy with existing KD methods

기존 KD 방법론이 JSD와 KLD에 Off-policy를 적용하게 되었을 때 효과가 제한적이며, 성능은 DISTILLM에 비해 낮다.

DISTILLM의 구성 요소인 SRKL과 Adaptive Off-policy는 서로 강한 시너지 효과를 가진다.

 

Appropriateness of adaptive probability

Adaptive SGO Scheduler로 설정된 확률값을 사용한 성능이 수동으로 정의한 확률값의 성능을 넘어섰으며, 이는 동적으로 상황에 맞는 최적의 확률값을 제공할 수 있음을 보여준다.

Adaptive SGO Scheduler에서 생성된 확률값은 수동으로 최적화된 확률값에 매우 근접하며, SKL의 경우 0.2 이하, SRKL의 경우 0.1 이하의 차이를 보였다.

 

One-stage Distillation

기존의 KD 방법론은 학생 모델이 생성한 SGO를 Fine-Tunning 하지 않는다면, 퇴화된 SGO를 생성하고, 노이즈 피드백을 유발한다.

하지만, DISTILLM은 미세 조정된 학생 모델을 시작점으로 사용할 필요가 없으며, 초기 상태(pretrained parameters)만으로도 KD를 수행할 수 있다.

DISTILLM은 학생 모델의 초기 상태에 관계없이 안정적인 성능을 유지하며, 다른 방법론과 달리 효율성을 지닌다.

 

Conclusion

Auto-Regressive Language Model을 위한 KD 프레임워크의 문제를 해결하기 위해 DISTILLM을 설계하였다.

DISTILLM은 SKL과 Adaptive Off-Policy Approach를 활용하여 다양한 생성 작업에서 학습 효율성 개선 및 성능 향상 등 우수한 성능을 입증하였다.

이를 통해 KD의 주요 문제점인 노이즈 피드백, 샘플 효율성 문제를 해결하며, 기존 프레임워크보다 우수한 성능과 효율성을 제공한다.