티스토리 뷰
임계값 변화에 따른 정밀도, 재현율 변화를 확인해보고, 정밀도와 재현율의 관계, F1 score에 대해 알아본다.
임계값 변화에 따른 평가지표 값의 변화 확인
타이타닉 데이터셋을 활용하여 평가지표를 확인해본다.
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import seaborn as sns
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, precision_score, recall_score, confusion_matrix
df = sns.load_dataset('titanic')
df_sp=df[['survived','pclass','age','sibsp','parch','fare']]
df_sp.dropna(inplace=True)
X_train, X_test, y_train, y_test = train_test_split(df_sp.drop('survived',axis=1), df_sp['survived'], test_size=0.3, random_state=111)
평가지표를 확인할 수 있는 함수를 구현하여 정확도, 정밀도, 재현율을 확인해본다.
# 평가지표 함수
def get_clf_eval(y_test, pred):
confusion = confusion_matrix(y_test, pred)
accuracy = accuracy_score(y_test, pred)
precision = precision_score(y_test, pred)
recall = recall_score(y_test, pred)
print('오차 행렬')
print(confusion)
print('정확도: {0:.4f}, 정밀도:{1:.4f}, 재현율:{2:.4f}'.format(accuracy, precision, recall))
lr_clf = LogisticRegression(solver='liblinear') # 데이터양이 적은 경우 사용하는 solver
lr_clf.fit(X_train,y_train)
pred = lr_clf.predict(X_test)
get_clf_eval(y_test, pred)
'''
오차 행렬
[[110 25]
[ 43 37]]
정확도: 0.6837, 정밀도:0.5968, 재현율:0.4625
'''# predict proba 값을 바탕으로 평가지표를 확인해본다.
pred_proba = lr_clf.predict_proba(X_test)
from sklearn.preprocessing import Binarizer
# binarizer 라이브러리를 통해 0과 1로 변환해서 반환할 예정
# theshold 지정하여 지정값보다 작거나 크면 0 또는 1로 반환을 해준다.
pred_proba[:,1].reshape(-1,1)
threshold = 0.4, 0.5, 0.6으로 변화를 주면서 평가지표를 계산한다.
thresholds= [0.3, 0.4, 0.5, 0.6, 0.7, 0.8]
def get_eval_threshold(y_test, pred_proba_1, thresholds):
for i in thresholds:
binarizer=Binarizer(threshold=i).fit(pred_proba_1)
pred =binarizer.transform(pred_proba_1)
print('임계값의 따른 평가지표', i)
get_clf_eval(y_test,pred)
get_eval_threshold(y_test,pred_proba[:,1].reshape(-1,1),thresholds)
'''
임계값의 따른 평가지표 0.3
오차 행렬
[[69 66]
[11 69]]
정확도: 0.6419, 정밀도:0.5111, 재현율:0.8625
임계값의 따른 평가지표 0.4
오차 행렬
[[94 41]
[30 50]]
정확도: 0.6698, 정밀도:0.5495, 재현율:0.6250
임계값의 따른 평가지표 0.5
오차 행렬
[[110 25]
[ 43 37]]
정확도: 0.6837, 정밀도:0.5968, 재현율:0.4625
임계값의 따른 평가지표 0.6
오차 행렬
[[123 12]
[ 50 30]]
정확도: 0.7116, 정밀도:0.7143, 재현율:0.3750
임계값의 따른 평가지표 0.7
오차 행렬
[[126 9]
[ 62 18]]
정확도: 0.6698, 정밀도:0.6667, 재현율:0.2250
임계값의 따른 평가지표 0.8
오차 행렬
[[129 6]
[ 67 13]]
정확도: 0.6605, 정밀도:0.6842, 재현율:0.1625
'''
임계값이 0.5보다 낮아졌을 때, 재현율이 올라가는 이유는 FN, FP 값들의 변화로 인해 발생하였다.
임계값이 낮아져 양성(생존)으로 예측을 많이 하게 되어, 실제 양성을 음성으로 예측하는 양이 줄어들게 된다.
정밀도와 재현율에 대한 관계를 확인한다.
from sklearn.metrics import precision_recall_curve
#레이블 값이 1일때 예측확률을 추출
pred_proba_class1 = lr_clf.predict_proba(X_test)[:,1]
# 실제값 데이터 세트와 레이블 값이 1일 때의 예측확률을 precision_recall_curve 인자로 입력
precisions, recalls, thresholds = precision_recall_curve(y_test, pred_proba_class1)
print('반환된 분류 결정 임곗값 배열의 shape:', thresholds.shape)
#반환된 임계값 배열 로우가 147건이므로 샘플로 10건만 추출하되, 임곗값을 15 step으로 추출
thr_index = np.arange(0,thresholds.shape[0],15)
print('샘플 추출을 위한 임계값 배열의 index 10개:', thr_index)
print('샘플용 10개의 임곗값:', np.round(thresholds[thr_index],2))
#15 step 단위로 추출된 임계값에 따른 정밀도와 재현율 값
print('샘플 임계값별 정밀도:', np.round(precisions[thr_index],3))
print('샘플 임계값별 재현율:', np.round(recalls[thr_index],3))
'''
반환된 분류 결정 임곗값 배열의 shape: (210,)
샘플 추출을 위한 임계값 배열의 index 10개: [ 0 15 30 45 60 75 90 105 120 135 150 165 180 195]
샘플용 10개의 임곗값: [0.06 0.18 0.22 0.25 0.28 0.29 0.32 0.35 0.4 0.46 0.51 0.57 0.68 0.86]
샘플 임계값별 정밀도: [0.372 0.395 0.422 0.435 0.468 0.496 0.528 0.546 0.554 0.56 0.617 0.733
0.7 0.667]
샘플 임계값별 재현율: [1. 0.988 0.975 0.925 0.9 0.862 0.812 0.738 0.638 0.525 0.462 0.412
0.262 0.125]
'''import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
%matplotlib inline
def precision_recall_curve_plot(y_test, pred_proba_c1):
# thredshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출
precision, recalls, thresholds = precision_recall_curve(y_test, pred_proba_c1)
#X축을 thredshold 값으로, Y축은 정밀도, 재현율 값으로 각각 plot 수행. 정밀도는 점선으로 표시
plt.figure(figsize=(8,6))
threshold_boundary = thresholds.shape[0]
plt.plot(thresholds, precision[0:threshold_boundary], linestyle='--', label='precision')
plt.plot(thresholds, recalls[0:threshold_boundary], label ='recall')
#thredshold 값 X축 Scale을 0.1단위로 변경
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1),2))
#X축, y축, label과 legend, 그리고 grid 설정
plt.xlabel('Threshold value'); plt.ylabel('Precision and Recall value')
plt.legend();plt.grid()
plt.show()
precision_recall_curve_plot(y_test, lr_clf.predict_proba(X_test)[:,1])
예측 임계값을 변화하면서 정밀도, 재현율 수치가 변경된다. 이때 trade-off가 일어난다.
단순히 평가지표 하나만을 보는 것이 아닌 종합적인 분석이 필요하다.
이는 도메인, 비즈니스에 따라 달라진다.
정밀도 높다는 의미는 최악의 경우에 확실한 기준인 경우에만 생존으로 예측한다는 의미를 내포할 수 있다.
정밀도는 확실한 생존자만 생존으로 예측하는 것이므로, 예측 절대치에 상관없이 1명만 제대로 예측하고, 나머지를 생존하지 않았다고 해도 100%의 값이 나올 수 있다.
재현율이 높다는 의미는 최악의 경우에 대부분의 사람들을 생존으로 예측했다는 의미를 내포할 수 있다.
전체를 모두 생존으로 예측했을 때, 예측한 사람 중 생존한 사람이 적더라도 재현율의 값은 100%가 나올 수 있다.
따라서, 재현율, 정밀도를 모두 확인해볼 필요가 있다.
재현율, 정밀도를 결합한 f1 스코어를 확인해본다.
from sklearn.metrics import f1_score
#평가지표 함수
def get_clf_eval(y_test, pred):
confusion = confusion_matrix(y_test, pred)
accuracy = accuracy_score(y_test, pred)
precision = precision_score(y_test, pred)
recall = recall_score(y_test, pred)
f1 = f1_score(y_test, pred)
print('오차 행렬')
print(confusion)
print('정확도: {0:.4f}, 정밀도:{1:.4f}, 재현율:{2:.4f}, f1:{2:.4f}'.format(accuracy, precision, recall, f1))
get_clf_eval(y_test, tt_pred_2)
'''
오차 행렬
[[123 12]
[ 50 30]]
정확도: 0.7116, 정밀도:0.7143, 재현율:0.3750, f1:0.3750
'''
ROC 커브 그래프를 확인해본다.
from sklearn.metrics import roc_curve
#레이블 값이 1일때의 예측 확률을 추출
pred_proba_class1 = lr_clf.predict_proba(X_test)[:,1]
fprs, tprs, thresholds = roc_curve(y_test, pred_proba_class1)
#반환된 임곗값 배열에서 샘플로 데이터를 추출하되, 임곗값을 5 step으로 추출
#thresholds[0]은 max(예측확률)+1로 임의 설정됨. 이를 제외하기 위해 np.arange는 1부터 시작
thr_index = np.arange(1, thresholds.shape[0],5)
print('샘플 추출을 위한 임곗값 배열의 index:', thr_index)
print('샘플 index로 추출한 임곗값:', np.round(thresholds[thr_index],2))
# 5step 단위로 추출된 임계값에 따른 TPR, FPR 값
print('샘플 임곗값별 FPR:', np.round(fprs[thr_index], 3))
print('샘플 임곗값별 TPR:', np.round(tprs[thr_index], 3))
'''
샘플 추출을 위한 임곗값 배열의 index: [ 1 6 11 16 21 26 31 36 41 46 51 56 61 66 71 76 81 86 91]
샘플 index로 추출한 임곗값: [1. 0.97 0.86 0.71 0.64 0.55 0.5 0.48 0.46 0.43 0.4 0.37 0.36 0.33
0.31 0.3 0.28 0.25 0.2 ]
샘플 임곗값별 FPR: [0. 0.022 0.044 0.059 0.081 0.119 0.185 0.215 0.259 0.274 0.304 0.341
0.356 0.415 0.452 0.489 0.556 0.711 0.844]
샘플 임곗값별 TPR: [0.012 0.062 0.125 0.212 0.338 0.438 0.462 0.5 0.525 0.575 0.65 0.675
0.738 0.788 0.825 0.862 0.9 0.938 0.975]
'''def roc_curve_plot(y_test, pred_proba_c1):
#임곗값에 따른 FPR, TPR값을 반환받음.
fprs, tprs, thresholds = roc_curve(y_test, pred_proba_c1)
#ROC 곡선을 그래프 곡선으로 그림
plt.plot(fprs, tprs, label='ROC')
#가운데 대각선 직선을 그림
plt.plot([0,1], [0,1], 'k--', label='Random')
#FPR X축의 Scale을 0.1 단위로 변경, X,Y축 명 설정 등
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start,end,0.1),2))
plt.xlim(0,1);plt.ylim(0,1)
plt.xlabel('FPR(1-Specificity)');plt.ylabel('TPR(Recall)')
plt.legend()
roc_curve_plot(y_test, pred_proba[:,1])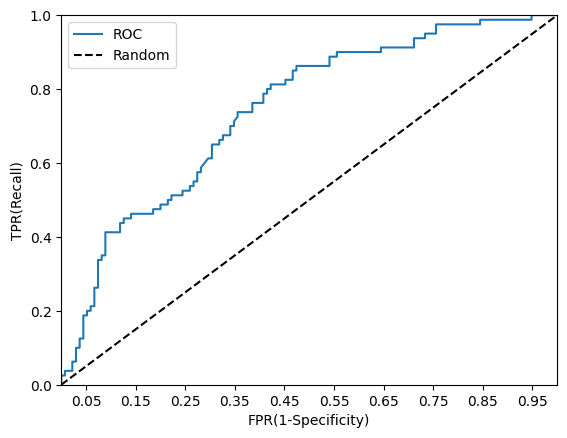
from sklearn.metrics import roc_auc_score
pred_proba = lr_clf.predict_proba(X_test)[:,1]
roc_score = roc_auc_score(y_test, pred_proba)
print('ROC AUC 값:{0:.4f}'.format(roc_score))
'''
ROC AUC 값:0.7425
''''B.D.A' 카테고리의 다른 글
| [BDA 데이터 분석 모델링반 (ML 1) 7회차] RFM 분석 (3) | 2024.06.05 |
|---|---|
| [BDA 데이터 분석 모델링반 (ML 1) 6회차] K-means 클러스터링 (1) | 2024.06.04 |
| [BDA 데이터 분석 모델링반 (ML 1) 5회차] KNN 알고리즘 (2) | 2024.06.03 |
| [BDA 데이터 분석 모델링반 (ML 1) 3회차] ML 평가지표 (1) | 2024.04.05 |
| [BDA 데이터 분석 모델링반 (ML 1) 2회차] Cross Validation (2) | 2024.03.25 |
- Total
- Today
- Yesterday
